Математические основы информатики

1. Информация и её свойства
2. Дискретная форма представления информации
3. Общие сведения о системах счисления
4. Восьмеричная и шестнадцатеричная системы счисления
5. Перевод десятичных чисел в другие системы счисления
6. Перевод чисел в десятичную систему счисления
7. Представление целых чисел в памяти компьютера
8. Представление вещественных чисел в памяти компьютера
9. Высказывания и логические операции
10. Построение таблиц истинности
11. Свойства логических операций

Информация и её свойства

Наука информатика изучает информацию. Хотя сам термин "информация" - это очень обширное понятие, и как такового строгого определения информации нет. Но все же с точки зрения информатики информация - это содержание тех сигнальных последовательностей, которые передаются в сети, по радио, между людьми или ещё где-нибудь еще.

Информация обладает следующими свойствами:

• адекватность
• актуальность
• доступность
• достоверность
• полнота
• понятность
• объективность

Более подробно с термином информация и с процессами, происходящими в информационно пространстве вокруг нас вы можете узнать из статьи "Информация и информационные процессы". В данной же статье мы не будем подробно останавливаться на этом вопросе.

Дискретная форма представления информации

В нашем мире широко распространены два вида представления информации - это дискретная и аналоговая.

Дискретное представление информации - это когда наш объект информации имеет только конечное множество значений. При этом сама это наша дискретная величина меняется скачкообразно.

Аналоговая форма представления информации имеет некоторый промежуток значений, но из этого промежутка значений она может принимать абсолютно любое значение. И меняться она может непрерывно.

Давайте приведем пример. У нас есть число от 0 до 10. В дискретном представлении это число может быть только целым числом, единицей, двойкой, тройкой и т.д.

В аналоговом представлении, если у нас будет тот же промежуток от 0 до 10, то аналоговая величина сможет иметь любое значение, например одну целую и  158 тясячных и так далее, в том числе даже иррациональное.

В памяти компьютера хранить аналоговую информацию практически невозможно,  в компьютере практически невозможно, поэтому мы применяем дискретную форму представления аналоговой информации.

Давайте придём более наглядный пример. Допустим, у нас есть метеорологическая станция, в которой ведутся записи температуры. Данные представлены плавным графиком, где по оси Х открладывается значение времени, а по оси Y значение температуры. Информация здесь храниться  в аналоговом виде.

Для любого конкретного времени мы всегда сможем посмотреть конкретную температуру. Хорошо, что информация очень точная, но при этом варианте хранения данные в компьютере будут занимать очень много места.

Для дискретного варианта представления мы просто разобьем наш график на конечное количество каких-то определенных моментов времени. И для этих моментов времени найдем температуру.

Мы получим в итоге конечное число значений, по которым, не имея исходного графика можно воспроизвести его и найти нужную температуру в нужный момент времени.

Платой за такое упрощение хранения данных является их точность. Для увеличения точности необходимо уменьшать промежутки снятия показаний с исходного графика.

Мы сможем взять столько точек, сколько нам нужно для достижения необходимой точности.

Общие сведения о системах счисления

Мы с вами в повседневной жизни используем числа и способ записи, которым мы эти числа записываем, и есть система счисления. Знаки, с помощью которых мы эти числа записываем называются цифрами, количество цифр в нашей системе счисления называется основанием. То есть основания - это то, сколько цифр в мы используем в нашей системе счисления для записи всех возможных чисел.

Это верно только для позиционных систем счисления. Также в природе существуют и непозиционные системы счисления.

Ярким примером непозиционных систем счисления  является так называемая Римская система счисления. Часто встречаются часы, на которых цифры написаны в непозиционной римской системе счисления. Как записываются числа в римской системе счисления? У нас есть некоторые базовые числа. Ещё C, которая обозначает сотню, есть М, которая обозначают тысячу и т.д.

Если рассмотреть пример записи числа 35, то видно, что знак Х(10) в независимости от позиции в числе обозначает именно 10.

ХХХV = 35

В позиционных системах, например, в хорошо знакомой нам десятичной, наоборот, от места записи цифры зависит, какое число единиц, десятков сотен или тысяч необходимо добавить к числу.

Для каждого числа в позиционной системе счисления существует расширенная запись, показывающая, из каких частей состоит наше исходное число.

135 = 1*10²+3*10¹+5*10⁰ = 100 + 30 + 5

Здесь мы умножаем каждый разряд на соответствующую степень десяти, потому что наша система счисления десятичная. Такую запись можно сделать и для любой другой системы, например, троичной или пятеричной.

Восьмеричная и шестнадцатеричная системы счисления

Сколько в нашей системе счисления цифр для записи чисел, то такое число и стоит в названии этой системы. Если для записи чисел мы используем только 8 цифр (01234567), то система будет называть восьмеричная. Давайте посмотрим, как будут записываться числа в такой системе счисления.

0₁₀=0₈

1₁₀=1₈

4₁₀=4₈

9₁₀=11₈

10₁₀=12₈

11₁₀=13₈

и т.д.

С числами в данной системе счисления можно проводить точно такие же математические действия, как и с десятичными числами.

11₈+17₈=30₈

При этом нужно помнить, что максимальное число, которое может стоять в одном разряде - это уже не 9, а 7. Соответственно, при выполнении операций необходимо переносить единицу в следующий разряд правильно.

В некоторых случаях проще сначала перевести заданные числа в десятичную систему, посчитать результат и перевести его обратно в восьмеричную.

Существуют в природе и более интересные системы, такие как шестнадцатеричная система счисления. Помимо обычных цифр, в ней используются буквы A, B, C, D, E, F

В таком случае запись чисел будет уже немного другой:

9₁₀=9₁₆

10₁₀=A₁₆

15₁₀=F₁₆

16₁₀=10₁₆

24₁₀=18₁₆

35₁₀=23₁₆

Мы познакомились с записью чисел в разных системах счисления. А теперь попробуем разобраться, как же переводить эти числа из одной системы в другую.

Перевод десятичных чисел в другие системы счисления

Попробуем перевести число 43 в двоичную систему счисления. Как нам известно, основанием двоичной системы является число 2. Ниже представлен способ перевода десятичного числа в двоичную систему счисления.

Принцип основан на постоянном делении исходного числа на 2 и нахождения остатка от этого деления. Именно остаток необходимо записывать в конечный результат.

43:2=21 (остаток 1)

21:2=10 (остаток 1)

10:2=5   (остаток 0)

5:2=5   (остаток 1)

2:2=1   (остаток 0)

Далее делить 1 на 2 не имеет смысла, поэтому мы можем записать ответ по следующему правилу:

Первой в ответ записывается результат деления 2 на 2, то есть единица и далее записываются найденные остатки, начиная  с самого последнего. В итоге получает такую запись числа 43.

43₁₀=101011₂

Чтобы перевести число в любую другую систему счисления, необходимо делить исходное число на нужное нам основание Q и находить остатки отделения, пока на последнем шаге не получится число, меньшее, чем основание системы, в которую мы переводим исходное число.

Например, попробуем перевести то же число 43 в шестнадцатеричную систему:

43:16=2 (остаток 11)

Таким образом, мы записываем сначала 2, а затем остаток 11 в нужной нам системе. Числу 11 в шестнадцатеричной системе соответствует буква В, потому так выглядит результат:

43₁₀=2В₁₆

Перевод чисел в десятичную систему счисления

Для перевода чисел из системы счисления с основанием Q в десятичную систему счисления нужно воспользоваться расширенной записью чисел, которую мы рассмотрели ранее.

Пусть у нас есть некоторое число в двоичной системе 1101, тогда для перевода этого числа в десятичную систему запишем его расширенную версию:

11012=1*2³+1*2²+0*2¹+1*2⁰=8+4+0+1=13₁₀

Здесь степени числа 2, которое является основанием двоичной системы соответствуют номеру разряда, в котором стоит 0 или 1, на которую мы умножаем двойку в степени.

Аналогично стоит поступать и с другими системами счисления.

Представление целых чисел в памяти компьютера

Как мы уже знаем, в нашем компьютере или в электронной вычислительной машине все числа хранятся в виде двоичного кода, то есть в последовательности нулей и единиц. Но что эти последовательности значат, и как определить, какие именно биты данных отвечают за определенные числа?

Обычно наш компьютер использует для хранения одного числа 8, 16, 32 или 64 разряда и бита. И если необходимо в память записать число 103₁₀, то компьютер сначала переводит его в двоичный код, а затем записываем в ячейку памяти, дополняя это число нулями:

00001101

В итоге получились те самые 8 бит или 1 байт.

Если мы хотим записывать в такие ячейки данных отрицательные числа, там нужно один из 8 битов отдать под этот знак. Соответственно числа мы можем записывать только в последние 8 бит, а знак (+ это 0, - это 1) мы запишем в восьмой бит.

Также можно найти, какой максимальное количество чисел мы можем хранить в ячейке памяти. Для этого необходимо число 2 возвести в степень, равную количеству значащих бит в ячейке данных.

Например, в ячейку данных размеров 16 бит можно записать 2₁₆= 65536 чисел

Представление вещественных чисел в памяти компьютера

Любое вещественное число можно представить в следующем виде

A = +- m*q^p

где m - это так называемая мантисса числа, q - это основание системы счисления, p - порядок числа.

Число 123000000 мы можем записать разными способами:

123,0*10⁶

12,3*10⁷

1,23*10⁸

Мантисса может быть представлена по-разному, но для удобства была введена договорённость, что мантисса всегда записывается так, чтобы целая часть была равна нулю, а потом записываются все остальные знаки.

Поэтому правильнее будет такое число записывать так:

0,123*10⁹

Такие числа удобно записывать в ячейки памяти от 16 бит и более.

При этом первые 8 бит отводятся на запись степени основания (1 бит знак степени и 7 бит  под значение степени). Остальные биты в ячейке отводятся на запись мантиссы (1 бит на знак мантиссы, остальное на значение).

Высказывания и логические операции

Высказывание - это некоторое повествовательное предложение, про которое мы точно можем сказать, истинно оно или ложно.

Например мы можем сказать «сейчас светит солнце» или мы можем сказать «сейчас идёт дождь». Оба эти высказывания одновременно истинными быть не могут. То есть сейчас либо идет дождь, либо светит Солнце. Одно из этих высказываний будет истинным, а  другое  в этом случае будет ложным.

Например, «дважды два равно пять» - это утверждение точно ложно, а «дважды два равно четыре» истинно.

Обычно в информатике ложь обозначают за 0, а истину за единицу.

Но не все предложения в нашем русском языке истинные или ложные. Есть вопросительное предложение или предложение, которое не несет в себе никакой информации с точки зрения информатики, например возглас «Стой!».

В нашем человеческом языке для связи частей предложения мы пользуемся союзами «и» или  «или».

В информатике это называется операциями. Давайте познакомимся с тремя логическими операциями, их также называют логическим умножением (конъюнкцией), сложением (дизъюнкцией) и отрицанием.

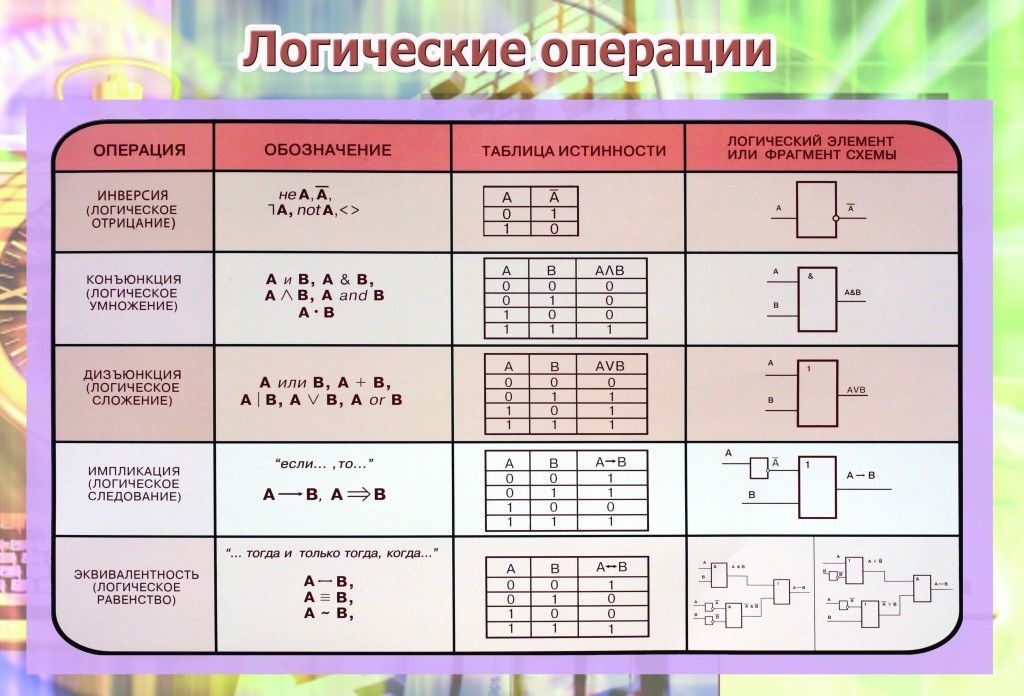
С помощью этих операций мы можем объединять простые высказывания в более сложные.

Построение таблиц истинности

Составив сложное высказывание из более простых высказываний с помощью знаков логических операций вы можете составить таблицу истинности, чтобы знать, какое значение будет принимать общее высказывание в зависимости от значения отдельных высказываний в этом большом высказывании.

Пример составления таблицы истинности для высказывания показан на рисунке.

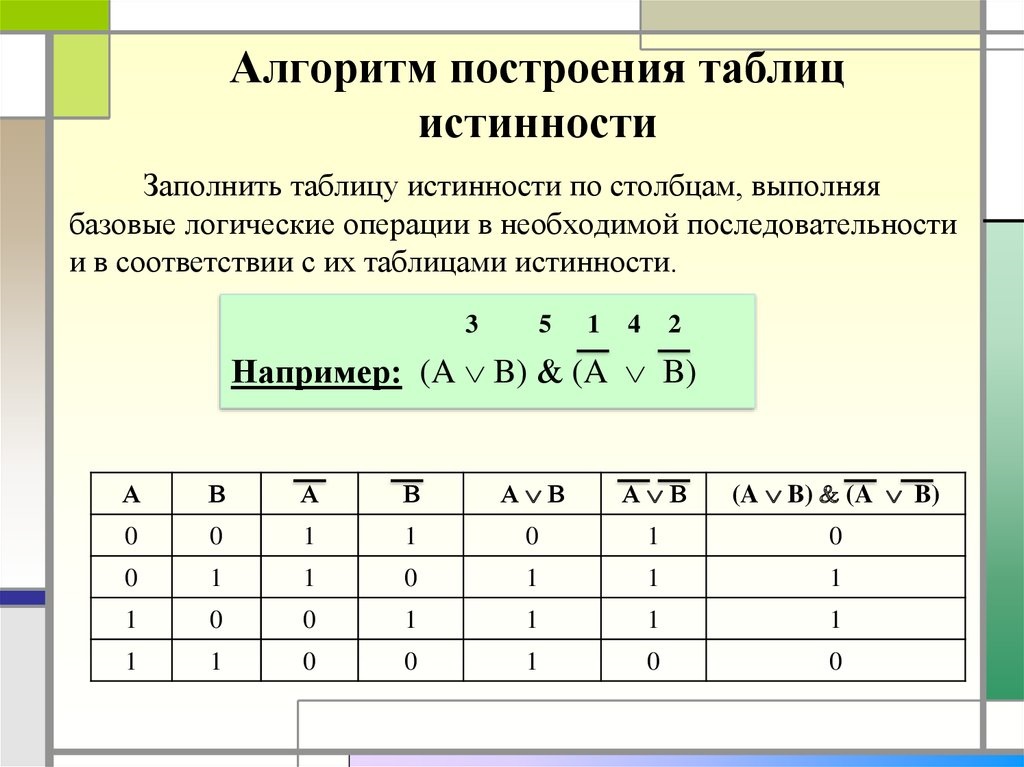
Обратите внимание, что поочередно находятся значения отдельных частей общего высказывания в соответствии с приоритетом применения логических операций.

Самый высший приоритет имеет операция отрицания, далее идет конъюнкция, а уже потом дизъюнкция.

Свойства логических операций

Также как и в математике, в информатике наши логические переменные и логические операции имеют некоторые свойства.

Во-первых, мы уже говорили о приоритете операций.

1 - отрицание (не)

2 -  конъюнкция (∩, &, и)

3 - дизъюнкция (∪, или)

Во-вторых, у логических операций есть некоторые свойства:

А∩0=0

А∪0=1

(не)А∪А=1

(не)А∩А=0

(не)(не)А=А

В-третьих, также как и в математике, для логических операций применяются переместительный, распределительный и сочетательный законы, а также закон полного отрицания:

А∩(В∪С)=А∩В∪А∩С

А∪В∩С=А∪В∩С

А∪В=В∪А

А∩В=В∩А

(А∩В)∩С=А∩(В∩С)

(А∪В)∪С=А∪(В∪С)

(не)(А∩В)=(не)А∪(не)В

(не)(А∪В)=(не)А∩ (не)В

Проверить любое из этих утверждений и свойств вы можете с помощью таблиц истинности.